Introduction to Radiance Calibrated Nighttime Light Data¶
This section is adapted from module 1, section 2 of Open Nighttime Lights.
DMSP-OLS Overview¶
Sensors aboard Defense Meteorological Satellite Program (DMSP) satellites have been providing low-light imaging of the Earth's surface since the 1960s, with a digital archive established in 1992 at NOAA's National Centers for Environmental Information (NCEI), formerly the National Geophysical Data Center (NGDC). The Operational Linescan System (OLS) onboard the DMSP satellites (DMSP-OLS) provided the primary data on nighttime lights until the introduction of the Joint Polar Satellite System (JPSS) program, which officially launched its first satellite in 2017. This JPSS program uses the Visible Infrared Imaging Radiometer Suite Day/Night Band (VIIRS-DNB) sensor, the first of which was launched aboard the S-NPP satellite in 2011 to serve as a transition between DMSP and JPSS. While the DMSP-OLS product was discontinued in 2014, the data stored in NOAA's archive still serves as the primary source of nighttime light data from 1992-2014, and as such is a valuable tool for academics and policy makers.
DMSP-OLS Usage and Limitations¶
While advanced for its time, the OLS is now old technology and was essentially unchanged since 1976 with the start of the Block 5D series of DMSP satellites. The OLS VIS, the low-light imaging band, has only 6-bit quantization (its digital values range from 0-63). The gain of the instrument, which is a multiplier on the signal (analogous to a volume setting), is adjusted on-the-fly onboard the satellite via an algorithm that takes into account the amount of expected moonlight and sunlight for the time and location. The dynamic gain adjustment of the OLS allows the VIS sensor to produce meaningful imagery under a wide range of conditions, from full sunlight during the day to a dark night with the moon below the horizon. The OLS gain states are not recorded in the global OLS data that is relayed back to the ground stations, making any downstream calibration difficult to achieve. The OLS VIS band has no on-board calibration, so the 64 (0-63) values are only relative values based on the gain in which the data were recorded. The lack of on-board calibration also means the the DMSP-OLS annual stable lights series derived from multiple OLS sensors and different years (1992–2013) are not comparable directly without inter-calibration.
For nighttime data, only imagery from nights with no moonlight present was included. Under no moonlight conditions, the dynamic gain algorithm sets the VIS gain to its maximum value. Using only these data gave some assurance that the gain was constant (albeit unknown) and that it was reasonable to temporally average these VIS band values. The high gain setting also meant that dimmer lights could be detected in the composites. The downside is that when the gain is set to its maximum value, the VIS band, with its 6-bit radiometric resolution, saturates over bright urban centers. This means all values have the maximum value of 63 leaving the variability within urban cores unresolvable (Figure 1.1).
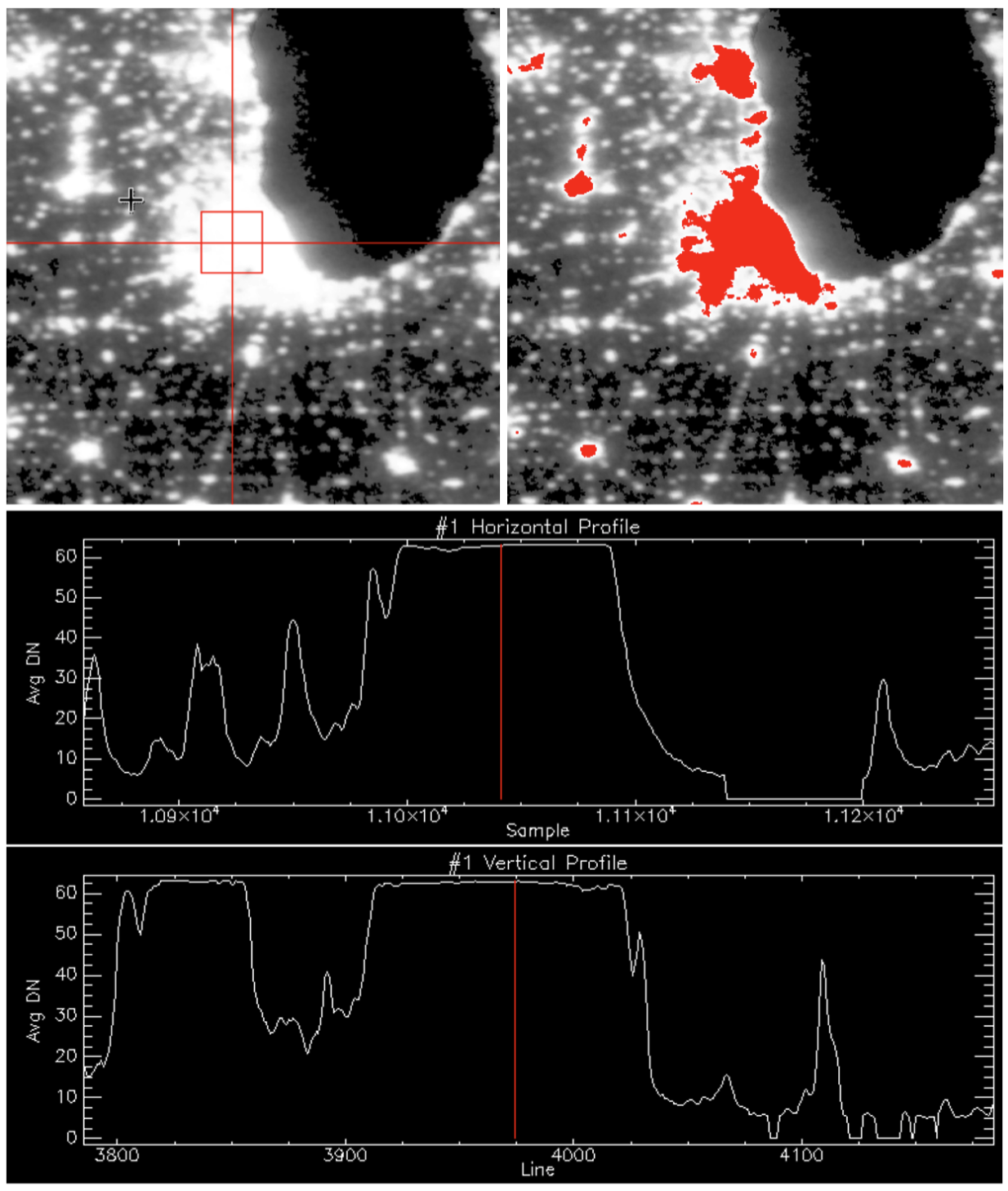
Figure 1.1 A subset of the F18 2013 stable lights composite over Chicago and surrounding communities illustrates the effect that saturation in the DMSP-OLS VIS band has on the information content in urban centers. The upper left image is a grayscale image where the horizontal and vertical red lines are the locations for the profile data plotted in the two charts. The upper right image is the same subset, but with saturated values colored red. Notice that most of the Chicago metropolitan area is saturated so no further detail is available using these data. The two charts are plots of transects through the image, showing the average DN value in the composite along horizontal and vertical tracks through Chicago. While there is variation in average DN values across the smaller towns, the larger urban cores are saturated.
Saturation occurs when pixels in bright areas, such as in city centers, reach the highest possible digital number (DN) value (i.e., 63) and no further details can be recognized.
Radiance Calibrated Nighttime Light Data¶
To account for the saturation of city centers in the DMSP-OLS nighttime light data, a limited set of observations were also collected with lower gain settings, making the sensor less sensitive to light. While this makes the sensor less able to identify dim lights, for the purposes of studying lighting within city boundaries it is a more useful source than the standard DMSP-OLS data. To provide this additional detail, the data collected from the sensors at lower gain levels were merged with the primary nighttime light product to recover the variation within bright areas. Radiance calibrated data are available from 1996 to 2010 at intervals of 1 to 4 years.
Given that the DMSP-OLS sensors had differing levels of sensitivity, the gain levels at which the sensors were set are not consistent across different satellites. When merging the radiance calibrated data, this is addressed by using the highest level of gain as a reference and weighting the lower-level gain data accordingly. This product is unitless due to the variable gain settings and a degredation in the sensors over time, and thus is recommended only for use which doesn't require numeric radiance values. Due to the differences in sensors and gain levels over time, it is necessary to perform inter-annual calibration to compare the radiance calibrated data from different years.